Author: Applied Macro

“It ain’t what you don’t know that gets you into trouble. It’s what you know for sure that just ain’t so.” Mark Twain

Definition

Dictionaries have a range of broadly related definitions, mostly suggesting the mathematical meaning and everyday sense are identical. As we saw with the word “significance” https://appliedmacro.com/2017/06/12/the-misuse-of-significance/, when there is no clear distinction in statistical and everyday usage, it can lead directly to confusion and often dangerous errors.

A few meanings:

• Historical origin of the word is likely from medieval Latin:
  
• Modern common usage, it is “a mutual relationship or connection between two things”
• In statistics, it broadly means a “quantity measuring the interdependence of variable quantities”.
• Here a difficulty arises, as although statistics has this broad meaning for it, often (especially in economics or finance) when people say correlation, they are talking about the Pearson Correlation Coefficient, also referred to as Pearson’s r.
• Person’s r is the formula I gave you in the previous posts (https://appliedmacro.com/2017/06/28/the-misuse-of-correlation-part-1-quick-refresher-and-quiz/) and is specifically a measure of linear correlation between two variables.
  It has a value between +1 and −1, where 1 is perfect positive linear correlation, 0 is no linear correlation, and −1 is perfect negative linear correlation.

Issues

I would like to deal with well-known issues that still lead to common mistakes.

1. Uncorrelated does not mean unrelated
2. Correlation does not imply causation
3. Correlation is not transitive
4. Data issues

I’ll deal with the first two in the remainder of this post, and the second two in the following, to keep the posts to a reasonable length.

1. Uncorrelated does not mean unrelated

Saying things are uncorrelated, people generally mean there is no relationship between them in everyday usage. Let’s look at a couple of examples where this common logic error leads to dangerously incorrect conclusions:

A). Relationships can be non-linear

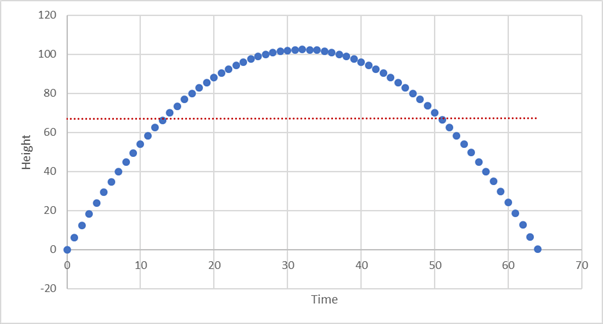
When a cannonball is fired, its path will form a parabola (OK strictly only in a vacuum!). If we look for a relationship between height and time, draw a chart then the relationship is very clear.

If we ran a Pearson r correlation analysis instead of drawing the picture, we would find there is ZERO correlation between height and time. Other statistical correlation measures, such Spearman’s rho which looks for monocity may pick up non-linear monotonic relationships, but also will not help you here for a parabolic relationship.

If you are using a statistical analysis early on in your investigations, the absence of a measurable correlation, such as a linear one, can lead you to assume there is not any relationship and thus discard and ignore a very valid but non-linear relationship. This is a serious problem.

As with “significance”, using the same word for a mathematical term that we use in everyday language can lead to serious mistakes. Once explained in this way, it may seem obvious but starting an analysis by filtering early, only looking for relationships with high correlations, remains shockingly common even with people that are aware of the problem.

B). There can be a logical relationship which is important

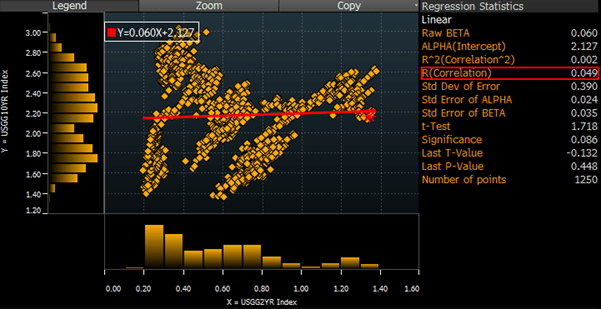
Take an example from financial markets, there is an intuitive connection between the short end and the long end of the bond market. If we look at US government bond yields 2 year (x-axis) versus 10 year (y-axis) over the last 5 years (chart below). The correlation between their levels is virtually zero and, if we were to only look at correlation, we may falsely conclude there is no relation between them.

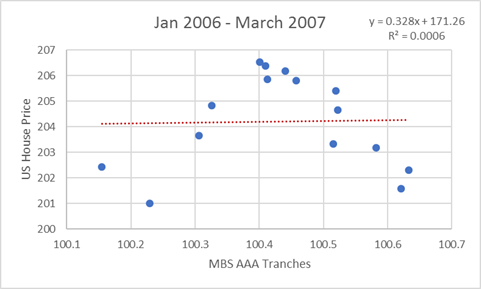
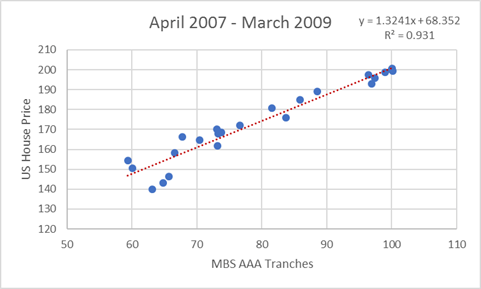
A more dramatic example with very dangerous consequences was the lack of a correlation between US house prices and the price of AAA tranches of mortgage backed securities before the crisis.

Before the crisis Correlation coefficient virtually zero

During the crisis Correlation coefficient = 0.96 (virtually 1!)

This was a very bad way to think about the relationship but a huge amount of money was invested on this poor assumption. It also relates to a serious logic flaw – just because something hasn’t happened in the past does not mean it can’t happen in the future.

2. Correlation does not imply causation

Everyone is taught this early in the study of statistics. Often with an example, as below, of a spuriously high correlation, where the intuitive relationship suggests something rather different.

https://www.mathsisfun.com/data/correlation.html

Everyone knows that ice cream and sunglasses have a common driver i.e. the weather. Perhaps it is less well known, how frequently this error is repeatedly made in economics and finance, even in the upper echelons of academia and policy making,

The policy impact and subsequent furore over the paper “Growth in a Time of Debt” by Carmen Reinhart and Ken Rogoff is a notable example. They found a correlation between national debt and growth rates, stating that “for levels of external debt in excess of 90%” GDP, growth was “roughly cut in half”.

On both sides of the political spectrum, the calculated correlation had become all that mattered:

• For those who wanted to reduce budget deficits in the US and UK, this was referred to as “conclusive empirical evidence” (Paul Ryan) and “convincing” (George Osborne). A strong correlation proved the case for austerity
• For their opponents, their attention was focused on the details of a data error which reduced the strength of the calculated relationship. The weak correlation proved there should be no restriction on debt levels.

Both sides of that argument were so simplistic, it was bizarre. This is not a fault of the original work, doing statistical analysis is a good idea, it is a fault of over-simplistic interpretations of its meaning.

The relationship between macro data and financial crises are similarly an area of extreme concern.

It may be true that there is a correlation between budget deficits and currency crises.

If you then conclude that budget deficits cause currency crises, then it is a quick jump to proposing that the way to prevent a currency crisis is to focus on the deficit and cut spending.

This of course fails to explore some crucial, causal links. If budget problems and currency weakness are both manifestations of a common underlying problem then treating one of the symptoms will not cure anything. Once again, an overly simplistic analysis based on correlations can lead to disastrous policy recommendations.

In this post, I want to talk about an insidious error that creeps in with the usage of correlation in finance.

FT lexicon supports the idea that:

“a correlation is said to be positive if movements between the two variables are in the same direction and negative if it moves in the opposite direction.”

This definition is not unusual, commonly seen in finance textbooks.

Occasionally the formula may be presented:

But caveats in using the formula will likely be absent or at the least hidden from view.
By that, I mean the terms and are critically important but this importance is rarely appreciated. [1]

In the previous post, I asked you about the correlation of the changes of the two assets in the chart below:

a. Positive correlation

b. Negative correlation

c. They are uncorrelated

d. Not sure (be honest!)

The most obvious answer is of course b)
One line goes up and the other goes down so this means they have a negative correlation. This is unfortunately strictly incorrect if you paid attention to the instruction to consider the “changes in the two assets”.

A good answer is d)
Given the amount of information I had supplied, it’s a perfectly reasonable one.

Because another answer is a)
The correlation of the changes in the variables is +1, PERFECT POSITIVE correlation
and the lines are going in the OPPOSITE direction!!

(If you doubt this result please look at the data and calculations in the sheet attached (download) and use the CORREL function in excel.)

b) is an intuitive answer but a) is the answer that a financial analyst would calculate. If you imagine of situations where you are being given financial advice, it is clear there could be an immediate conflict!


First insidious confusion – the importance of the mean

If you have never seen this before, you may think I am lying or this is a convoluted trick. But it rests upon one key part of the calculation of correlation that is missing from virtually every definition I see, and is certainly missing from the vast bulk of work done by analysts in the finance industry.

The key is that correlation is calculated by looking at the relationship in deviations from the means (the terms and in the complicated mathematical equation).

In our example, the changes in the two variables in the chart have equal and opposite means, and so trend in different directions. However, the day to day volatility (deviation from the mean of the changes) is identical for both variables, and it is this term that drives the correlation whilst having no impact on the trend.

Here is a scatterplot of the % changes for each variable. Observe all the dots are distributed along the line – a perfect POSITIVE correlation.

This has a clear relationship to the way we think about the change in market prices of any asset:

In financial markets, the daily noise is usually much greater than the daily trend, and so forms the focus of most market commentary.

The key result is that if the noise term correlates for two assets, then they will correlate irrespective of their underlying trend, given the way correlation is calculated.
i.e. they could end up in very different places even if they are positively correlated!

Second insidious confusion – levels vs changes

The second insidious confusion can arise from a reference to correlation of the CHANGES or a correlation in the LEVELS of the two variables.

In financial markets, the method invariably used is to look at the changes in variables. In our example, we get the answer of positive 1 i.e. perfect positive correlation.

If we calculate the correlation using the levels or prices, we get an answer of -0.97
i.e. strong negative correlation

The intuitive result is the opposite of the result most likely to be calcuated by financial analysts.

Why does finance prefer the use the correlation of changes?

It is done for good reason. When you are looking at data with strong trends, as a lot of asset prices do, the correlation of levels can yield very strange results. Let’s take an example.

Let’s look at the US equity market (S&P 500 price – white line) and its PE ratio (orange line) over the last 30 years.

If we first look at the correlation of levels, we get a correlation of virtually zero.
This suggests a rather unintuitive result that there is no meaningful correlation between PE ratio and equity prices!

If we instead look at the correlation of changes, we get that there is a meaningful positive correlation of 0.78 which makes a lot more sense.

Conclusion

If these differences in the correlation results is were just some statistical fluke, from a couple of silly examples, then it would not matter.
But it is not an unusual result and it occurs when looking at the biggest and most commonly traded financial markets. It is therefore critical to avoid confusions such as these when thinking about what type of correlation to use or, more often, what someone else has used in the analysis you are reading.

---

[1] I very much enjoyed this paper by Francois-Serge Lhabitant which explains this issue very well. http://www.edhec-risk.com/edhec_publications/all_publications/RISKReview.2011-09-07.3757/attachments/EDHEC_Working_Paper_Correlation_vs_Trends_F.pdf

First, let’s refresh our memories of what correlation means.
This may seem very basic right now, but I would like to make sure the meaning is clear before we move on to its use.

I have included a question at the end, once you have read and thought about the definition:

• A definition from the FT Lexicon:
  “a correlation is said to be positive if movements between the two variables are in the same direction and negative if it moves in the opposite direction.”

• You can read examples in a number of sources such as

https://www.mathsisfun.com/data/correlation.html

and
http://www.bbc.co.uk/schools/gcsebitesize/maths/statistics/scatterdiagramsrev2.shtml

Here is a range of correlations, shown via a scatterplot:

Some important concepts

• A positive correlation is “when the values increase together”
  An example would be temperature and ice cream sales as “warmer weather and higher sales go together”.
• A negative correlation is “when one value increases and the other decreases”
  Note this is sometimes called an “inverse correlation”.
  An example would be weight of a car and its fuel efficiency as “cars that are heavier tend to get less miles per gallon.”
• No correlation is when “there is no connection”. An example would be IQ and house number.”

• For those of you with a more formal approach the mathematical formula for correlation is:
  
• In practice, most of us find it much easier to use the function CORREL() in Excel!

Question time

Here is an example with two asset prices A and B. When we represent the data in a chart it can often be done in one of two ways.

This chart has two lines, showing how both the prices of asset A and B moved over time.

The other way to chart this is to put the prices of A and B on the two axes instead. It looks like this.

To make sure you have understood the basic concept of correlation, I would appreciate it if you could vote on an answer to the following question. (all anonymous of course!)